How To Draw Electric Field Lines And Equipotential Lines

148 19.4 Equipotential Lines

Summary

• Explain equipotential lines and equipotential surfaces.
• Describe the activeness of grounding an electrical appliance.
• Compare electrical field and equipotential lines.

We can represent electric potentials (voltages) pictorially, just every bit we drew pictures to illustrate electric fields. Of class, the ii are related. Consider Figure i, which shows an isolated positive indicate charge and its electric field lines. Electric field lines radiate out from a positive charge and terminate on negative charges. While we use blue arrows to represent the magnitude and direction of the electric field, we employ green lines to represent places where the electric potential is constant. These are called equipotential lines in ii dimensions, or equipotential surfaces in three dimensions. The term equipotential is also used as a noun, referring to an equipotential line or surface. The potential for a bespeak charge is the same anywhere on an imaginary sphere of radius $latex \boldsymbol{r} $ surrounding the charge. This is truthful since the potential for a betoken charge is given by $latex \boldsymbol{Five = kQ/r} $ and, thus, has the aforementioned value at whatever bespeak that is a given distance $latex \boldsymbol{r} $ from the charge. An equipotential sphere is a circumvolve in the two-dimensional view of Figure 1. Since the electric field lines point radially away from the charge, they are perpendicular to the equipotential lines.

Effigy one. An isolated indicate charge Q with its electric field lines in blue and equipotential lines in green. The potential is the same along each equipotential line, meaning that no work is required to move a charge anywhere along one of those lines. Work is needed to move a charge from one equipotential line to another. Equipotential lines are perpendicular to electrical field lines in every case.

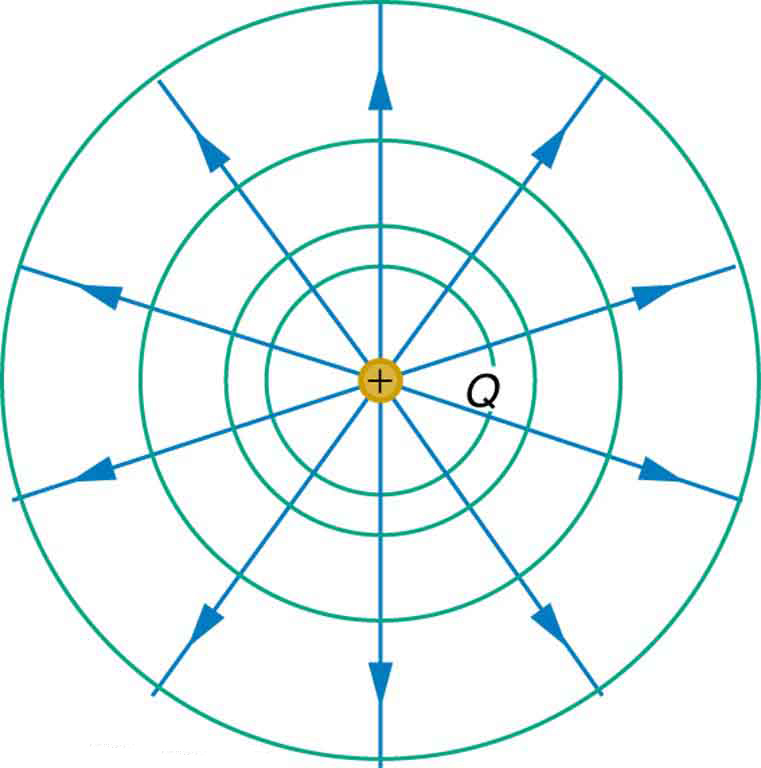
It is important to notation that equipotential lines are always perpendicular to electric field lines. No work is required to movement a charge along an equipotential, since $latex \boldsymbol{\Delta V = 0}$. Thus the work is

$latex \boldsymbol{W = – \Delta \;\textbf{PE} = -q \Delta V = 0}. $

Work is cypher if forcefulness is perpendicular to movement. Strength is in the aforementioned direction every bit $latex \boldsymbol{E}$, so that motion along an equipotential must be perpendicular to $latex \boldsymbol{E}$. More precisely, work is related to the electric field past

$latex \boldsymbol{W = Fd \;\textbf{cos} \theta = qEd \;\textbf{cos} \theta = 0.} $

Note that in the above equation, $latex \boldsymbol{E}$ and $latex \boldsymbol{F}$ symbolize the magnitudes of the electrical field strength and force, respectively. Neither $latex \boldsymbol{q} $ nor $latex \textbf{E} $ nor $latex \boldsymbol{d} $ is goose egg, and so $latex \boldsymbol{\textbf{cos} \theta}$ must be 0, pregnant $latex \boldsymbol{\theta}$ must be $latex \boldsymbol{ninety ^{\circ}} $. In other words, move along an equipotential is perpendicular to $latex \boldsymbol{E}$.

One of the rules for static electrical fields and conductors is that the electrical field must be perpendicular to the surface of any conductor. This implies that a usher is an equipotential surface in static situations. At that place tin can exist no voltage difference across the surface of a conductor, or charges volition flow. One of the uses of this fact is that a usher can exist fixed at zilch volts by connecting it to the earth with a good conductor—a process called grounding. Grounding can be a useful condom tool. For example, grounding the metal case of an electrical appliance ensures that it is at naught volts relative to the earth.

Grounding

A conductor can be fixed at nil volts by connecting it to the earth with a good conductor—a process called grounding.

Because a conductor is an equipotential, it can supervene upon any equipotential surface. For example, in Figure one a charged spherical conductor can replace the signal charge, and the electric field and potential surfaces outside of it volition exist unchanged, confirming the contention that a spherical accuse distribution is equivalent to a betoken charge at its eye.

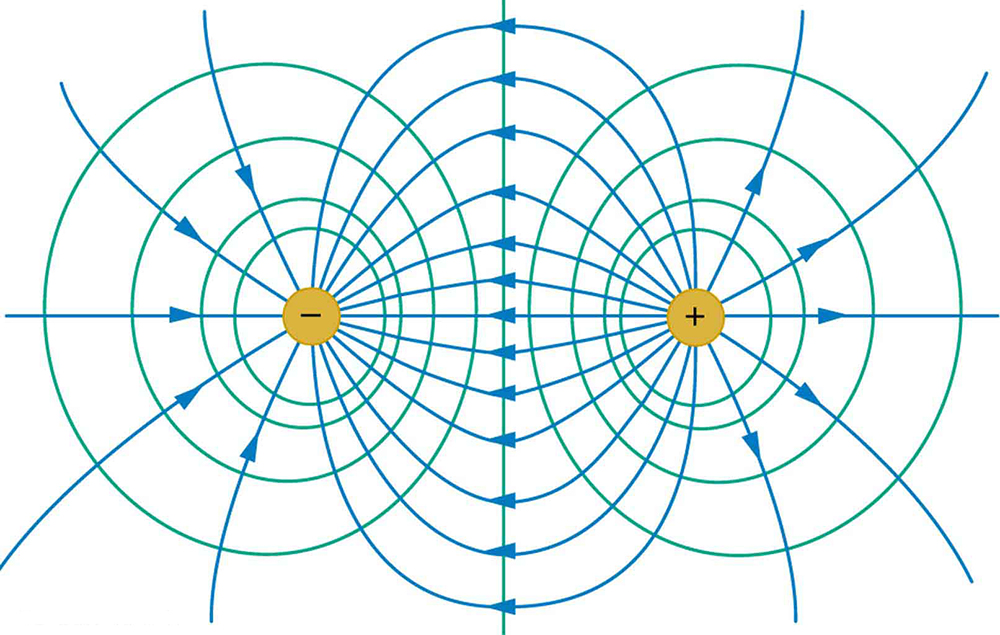
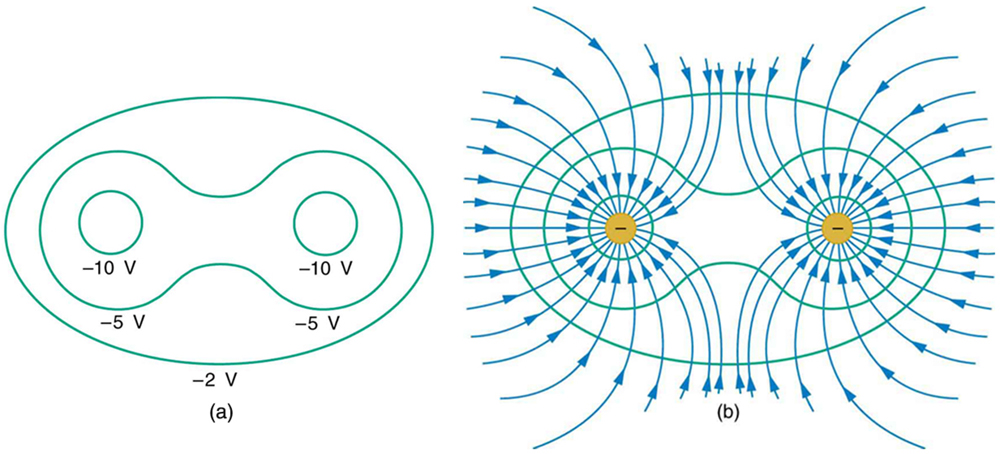
Figure ii shows the electric field and equipotential lines for two equal and opposite charges. Given the electric field lines, the equipotential lines tin can exist fatigued but past making them perpendicular to the electrical field lines. Conversely, given the equipotential lines, as in Figure 3(a), the electric field lines tin be drawn by making them perpendicular to the equipotentials, as in Figure 3(b).

Figure 2. The electric field lines and equipotential lines for ii equal but opposite charges. The equipotential lines tin can be fatigued by making them perpendicular to the electric field lines, if those are known. Note that the potential is greatest (well-nigh positive) well-nigh the positive charge and least (nearly negative) virtually the negative charge.

Figure 3. (a) These equipotential lines might be measured with a voltmeter in a laboratory experiment. (b) The corresponding electric field lines are found by drawing them perpendicular to the equipotentials. Notation that these fields are consistent with two equal negative charges

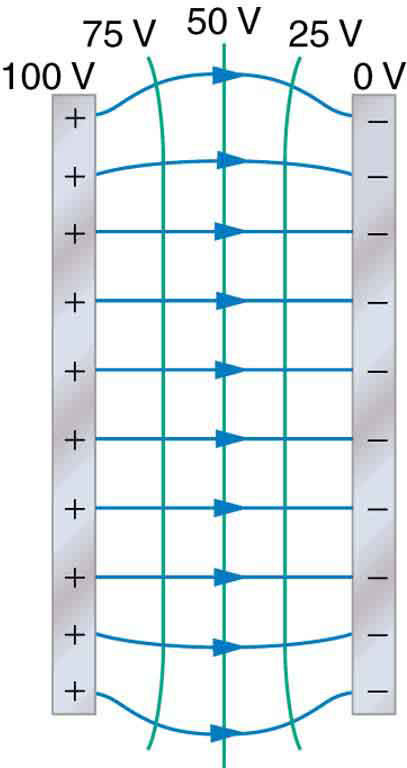
One of the most important cases is that of the familiar parallel conducting plates shown in Effigy 4. Betwixt the plates, the equipotentials are evenly spaced and parallel. The same field could exist maintained by placing conducting plates at the equipotential lines at the potentials shown.

Figure 4. The electric field and equipotential lines between 2 metal plates.

An important application of electric fields and equipotential lines involves the middle. The center relies on electric signals to maintain its rhythm. The movement of electric signals causes the chambers of the heart to contract and relax. When a person has a heart attack, the movement of these electrical signals may be disturbed. An artificial pacemaker and a defibrillator can be used to initiate the rhythm of electrical signals. The equipotential lines around the middle, the thoracic region, and the axis of the center are useful ways of monitoring the construction and functions of the center. An electrocardiogram (ECG) measures the small electric signals being generated during the action of the eye. More about the relationship betwixt electric fields and the heart is discussed in Chapter 19.7 Energy Stored in Capacitors.

PhET Explorations: Charges and Fields

Move point charges around on the playing field and and then view the electric field, voltages, equipotential lines, and more than. It'due south colorful, it's dynamic, it's free.

Figure 5. Charges and Fields

Section Summary

• An equipotential line is a line forth which the electric potential is abiding.
• An equipotential surface is a 3-dimensional version of equipotential lines.
• Equipotential lines are ever perpendicular to electric field lines.
• The procedure by which a conductor tin can be fixed at zero volts past connecting it to the globe with a skillful usher is called grounding.

Conceptual Questions

i: What is an equipotential line? What is an equipotential surface?

2: Explain in your ain words why equipotential lines and surfaces must be perpendicular to electric field lines.

3: Tin can different equipotential lines cross? Explicate.

Bug & Exercises

ane: (a) Sketch the equipotential lines almost a point charge + $latex \boldsymbol{q} $. Indicate the direction of increasing potential. (b) Practice the aforementioned for a bespeak charge $latex \boldsymbol{-3 \; q}$.

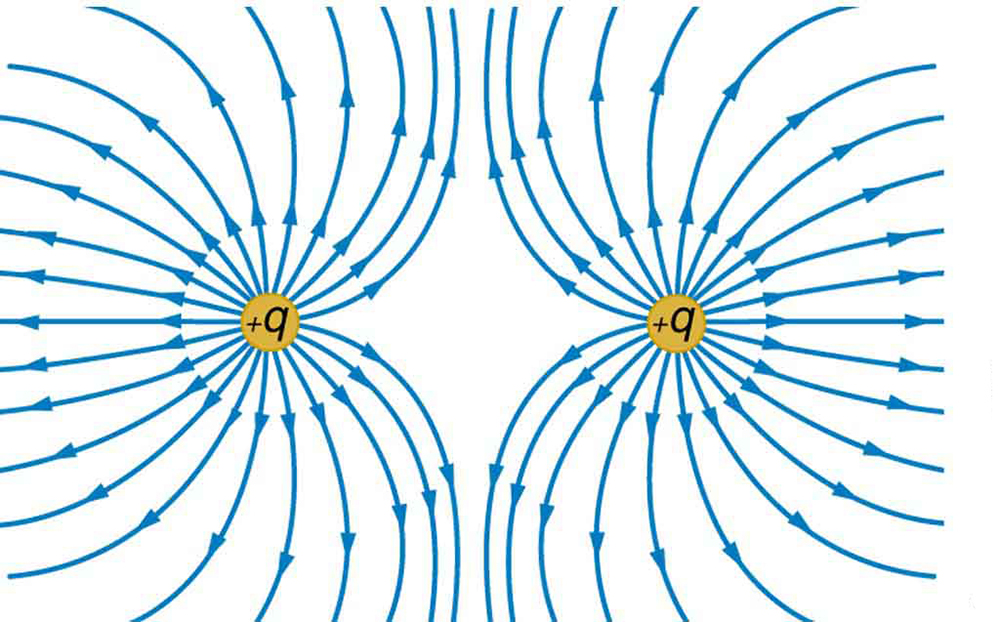
2: Sketch the equipotential lines for the 2 equal positive charges shown in Figure vi. Bespeak the direction of increasing potential.

Figure six. The electrical field virtually two equal positive charges is directed away from each of the charges.

iii: Figure 7 shows the electric field lines near two charges $latex \boldsymbol{q_1} $ and $latex \boldsymbol{q_2} $, the first having a magnitude iv times that of the 2nd. Sketch the equipotential lines for these two charges, and indicate the direction of increasing potential.

4: Sketch the equipotential lines a long distance from the charges shown in Effigy 7. Bespeak the direction of increasing potential.

Figure 7. The electric field near two charges.

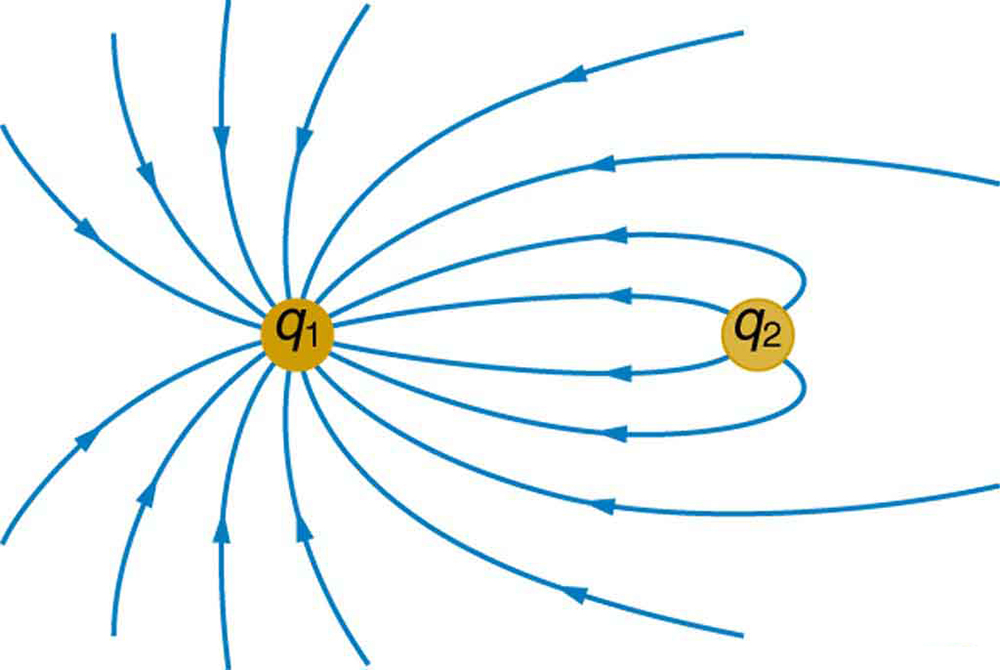
5: Sketch the equipotential lines in the vicinity of two opposite charges, where the negative accuse is three times as nifty in magnitude equally the positive. See Figure 7 for a similar situation. Indicate the direction of increasing potential.

six: Sketch the equipotential lines in the vicinity of the negatively charged conductor in Figure 8. How will these equipotentials look a long altitude from the object?

Figure 8. A negatively charged conductor.

7: Sketch the equipotential lines surrounding the two conducting plates shown in Figure 9, given the acme plate is positive and the bottom plate has an equal amount of negative charge. Exist sure to betoken the distribution of charge on the plates. Is the field strongest where the plates are closest? Why should it be?

Figure 9.

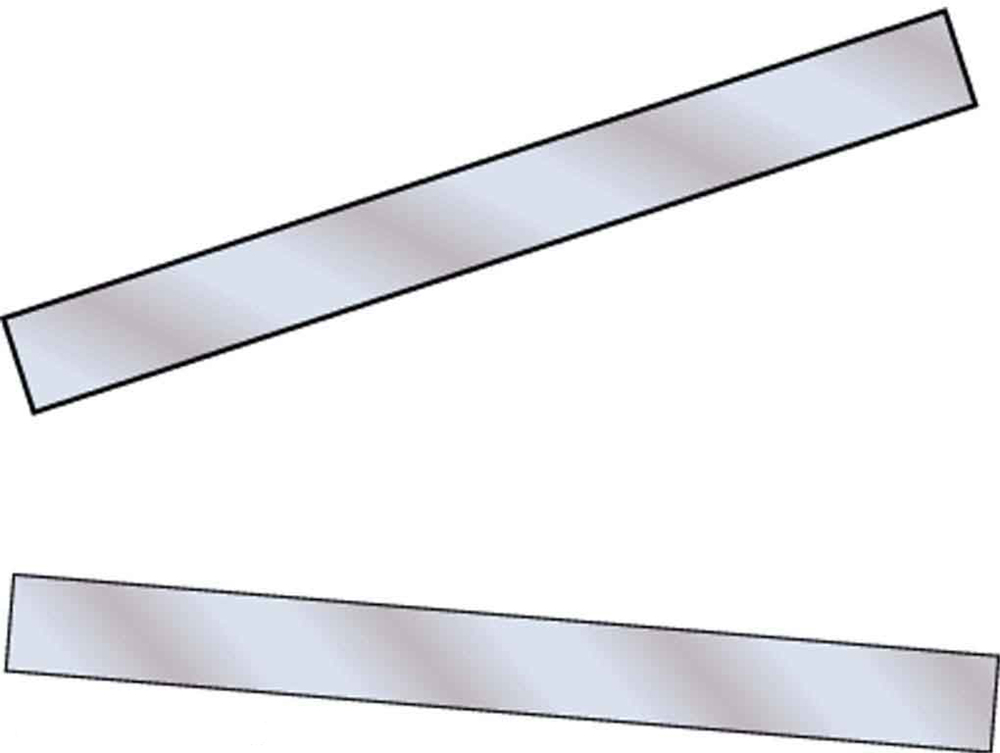
8: (a) Sketch the electric field lines in the vicinity of the charged insulator in Figure 10. Note its non-uniform accuse distribution. (b) Sketch equipotential lines surrounding the insulator. Indicate the direction of increasing potential.

Figure 10. A charged insulating rod such every bit might be used in a classroom demonstration.

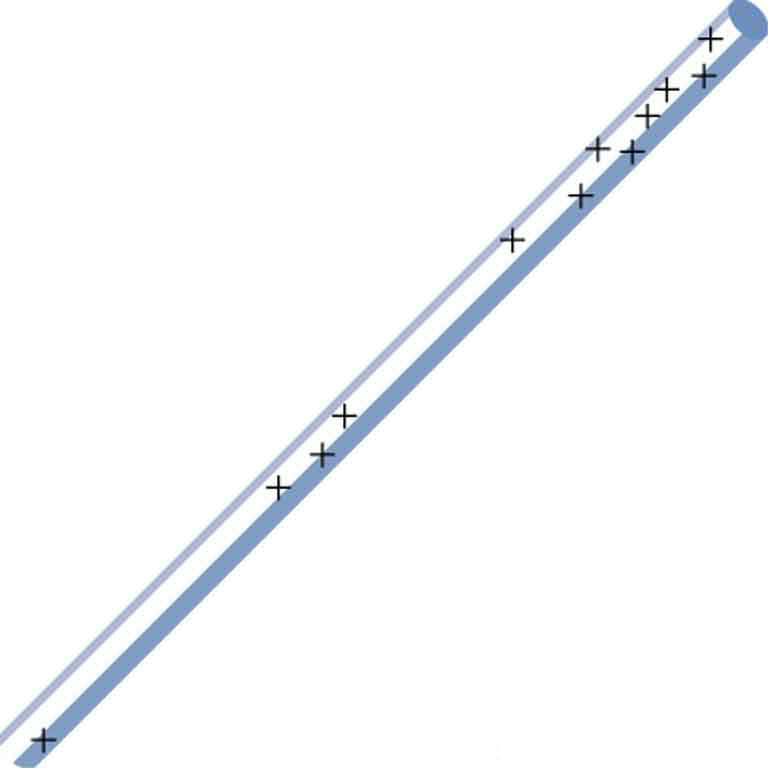
nine: The naturally occurring charge on the ground on a fine 24-hour interval out in the open land is $latex \boldsymbol{-1.00 \;\textbf{nC} / \textbf{m}^ii} $. (a) What is the electrical field relative to ground at a height of 3.00 m? (b) Calculate the electric potential at this pinnacle. (c) Sketch electric field and equipotential lines for this scenario.

ten: The lesser electric ray (Narcine bancroftii) maintains an incredible accuse on its head and a charge equal in magnitude but reverse in sign on its tail (Figure 11). (a) Sketch the equipotential lines surrounding the ray. (b) Sketch the equipotentials when the ray is near a ship with a conducting surface. (c) How could this charge distribution exist of use to the ray?

Figure 11. Lesser electric ray (Narcine bancroftii) (credit: National Oceanic and Atmospheric Assistants, NOAA's Fisheries Drove).

Glossary

equipotential line

a line along which the electric potential is constant

grounding

fixing a conductor at nil volts by connecting it to the earth or ground

Source: https://pressbooks.uiowa.edu/clonedbook/chapter/equipotential-lines/

Posted by: sandovalmeir1997.blogspot.com

Share this post